Поток - Flux

эта статья требует внимания специалиста по физике. Конкретная проблема: путаница между потоком и плотностью потока. Увидеть страница обсуждения для подробностей. ВикиПроект Физика может помочь нанять эксперта. (Сентябрь 2016)

Поток описывает любой эффект, который кажется проходящим или перемещающимся (независимо от того, движется он на самом деле или нет) через поверхность или вещество. Поток - это концепция в Прикладная математика и векторное исчисление который имеет множество приложений для физика. Для явления переноса, поток - это вектор количество, описывающее величину и направление потока вещества или свойства. В векторное исчисление поток - это скаляр количество, определяемое как поверхностный интеграл перпендикулярной составляющей векторное поле над поверхностью.^[1]

Терминология

Слово поток происходит от латинский: флюксус означает "поток", и дымоход это «течь».^[2] Так как текучесть, этот термин был введен в дифференциальное исчисление от Исаак Ньютон.

Концепция теплового потока была ключевым вкладом Жозеф Фурье, при анализе явлений теплопередачи.^[3] Его основополагающий трактат Теория аналитик де ла шалёр (Аналитическая теория тепла),^[4] определяет текучесть в качестве центральной величины и приступает к получению теперь хорошо известных выражений потока в терминах разницы температур на пластине, а затем в более общем плане в терминах температурных градиентов или разностей температур в других геометрических формах. Можно было бы возразить, основываясь на работе Джеймс Клерк Максвелл,^[5] что определение транспорта предшествует определение потока, используемого в электромагнетизме. Конкретная цитата Максвелла:

В случае потоков мы должны взять интеграл по поверхности от потока через каждый элемент поверхности. Результат этой операции называется поверхностный интеграл флюса. Он представляет собой количество, которое проходит через поверхность.

— Джеймс Клерк Максвелл

Согласно определению транспорта, поток может быть одним вектором или векторным полем / функцией положения. В последнем случае поток можно легко интегрировать по поверхности. Напротив, согласно определению электромагнетизма, поток является интеграл по поверхности; нет смысла интегрировать поток второго определения, так как один будет интегрировать по поверхности дважды. Таким образом, цитата Максвелла имеет смысл только в том случае, если «поток» используется в соответствии с определением транспорта (и, кроме того, это векторное поле, а не одиночный вектор). Это иронично, потому что Максвелл был одним из главных разработчиков того, что мы теперь называем «электрическим потоком» и «магнитным потоком» согласно определению электромагнетизма. Их имена в соответствии с цитатой (и определением переноса) будут «поверхностный интеграл электрического потока» и «поверхностный интеграл магнитного потока», и в этом случае «электрический поток» вместо этого будет определяться как «электрическое поле» и «магнитный поток». «определяется как« магнитное поле ». Это означает, что Максвелл воспринимал эти поля как потоки / потоки некоторого вида.

Учитывая поток согласно определению электромагнетизма, соответствующий плотность потока, если этот термин используется, относится к его производной по поверхности, которая была интегрирована. Посредством Основная теорема исчисления соответствующие плотность потока является потоком согласно определению транспорта. Учитывая текущий например, электрический ток - заряд за раз, плотность тока также будет потоком согласно определению переноса - заряд за время на площадь. Из-за противоречивых определений поток, и взаимозаменяемость поток, течь, и текущий в нетехническом английском языке все термины, используемые в этом абзаце, иногда используются взаимозаменяемо и неоднозначно. В остальной части этой статьи бетонные флюсы будут использоваться в соответствии с их широким признанием в литературе, независимо от того, какому определению флюса соответствует этот термин.

Поток как расход на единицу площади

В явления переноса (теплопередача, массообмен и динамика жидкостей ) поток определяется как скорость потока собственности на единицу площади, который имеет Габаритные размеры [количество] · [время]⁻¹·[площадь]⁻¹.^[6] Площадь - это поверхность, «через которую» проходит собственность. Например, величина речного течения, то есть количество воды, протекающей через поперечное сечение реки каждую секунду, или количество солнечной энергии, попадающей на участок земли каждую секунду, являются разновидностями потока.

Общее математическое определение (транспорт)

Вот 3 определения в порядке возрастания сложности. Каждый из них является частным случаем следующего. Во всех случаях частый символ j, (или J) используется для флюса, q для физическое количество что течет, т на время, и А для площади. Эти идентификаторы будут выделены жирным шрифтом только тогда, когда они являются векторами.

Во-первых, поток как (единичный) скаляр:

${ displaystyle j = { frac {I} {A}}}$

где:

${ displaystyle I = lim limits _ { Delta t rightarrow 0} { frac { Delta q} { Delta t}} = { frac { mathrm {d} q} { mathrm {d} t}}}$

В этом случае поверхность, на которой измеряется поток, является фиксированной и имеет площадь А. Предполагается, что поверхность плоская, а поток везде постоянный по отношению к положению и перпендикулярен поверхности.

Во-вторых, поток как скалярное поле определенная вдоль поверхности, т.е. функция точек на поверхности:

${ Displaystyle J ( mathbf {p}) = { frac { partial I} { partial A}} ( mathbf {p})}$

${ displaystyle I (A, mathbf {p}) = { frac { mathrm {d} q} { mathrm {d} t}} (A, mathbf {p})}$

Как и прежде, поверхность считается плоской, а течение всюду перпендикулярно ей. Однако поток не обязательно должен быть постоянным. q теперь функция п, точка на поверхности и А, площадь. Вместо того, чтобы измерять общий поток через поверхность, q измеряет поток через диск с площадью А сосредоточен на п по поверхности.

Наконец, поток как векторное поле:

${ displaystyle mathbf {j} ( mathbf {p}) = { frac { partial mathbf {I}} { partial A}} ( mathbf {p})}$

${ displaystyle mathbf {I} (A, mathbf {p}) = { underset { mathbf { hat {n}}} { operatorname {arg , max}}} , mathbf { hat {n}} _ { mathbf {p}} { frac { mathrm {d} q} { mathrm {d} t}} (A, mathbf {p}, mathbf { hat {n}} )}$

В этом случае нет фиксированной поверхности, над которой мы проводим измерения. q является функцией точки, площади и направления (заданного единичным вектором, ${ Displaystyle mathbf { шляпа {п}}}$), и измеряет поток через диск площади A, перпендикулярной этому единичному вектору. я определяется выбором единичного вектора, который максимизирует поток вокруг точки, потому что истинный поток максимизируется через диск, который перпендикулярен ему. Таким образом, единичный вектор однозначно максимизирует функцию, когда он указывает в «истинном направлении» потока. [Строго говоря, это злоупотребление обозначениями потому что "arg max" не может напрямую сравнивать векторы; вместо этого мы берем вектор с наибольшей нормой.]

Свойства

Эти прямые определения, особенно последние, довольно громоздки. Например, конструкция argmax является искусственной с точки зрения эмпирических измерений, когда Флюгер или аналогичный, можно легко определить направление потока в точке. Вместо прямого определения векторного потока часто бывает более интуитивно понятным указать некоторые его свойства. Кроме того, по этим свойствам в любом случае можно однозначно определить поток.

Если флюс j проходит через площадь под углом θ к нормали площади ${ Displaystyle mathbf { шляпа {п}}}$, тогда

${ Displaystyle mathbf {j} cdot mathbf { hat {n}} = j cos theta}$

где · это скалярное произведение единичных векторов. То есть составляющая потока, проходящего через поверхность (т.е. нормальная к ней), равна j cos θ, а составляющая потока, проходящего по касательной к площади, равна j sin θ, но есть нет поток действительно проходит через площадь в тангенциальном направлении. В только Компонента потока, проходящего по нормали к площади, является составляющей косинуса.

Для векторного потока поверхностный интеграл из j через поверхность S, дает правильное течение в единицу времени через поверхность.

${ displaystyle { frac { mathrm {d} q} { mathrm {d} t}} = iint _ {S} mathbf {j} cdot mathbf { hat {n}} , { rm {d}} A = iint _ {S} mathbf {j} cdot { rm {d}} mathbf {A}}$

А (и его бесконечно малый) - это векторная площадь, сочетание площади, через которую проходит недвижимость, А, а единичный вектор нормально к области, ${ Displaystyle mathbf { шляпа {п}}}$. Отношение ${ Displaystyle mathbf {A} = A mathbf { шляпа {п}}}$.В отличие от второй системы уравнений, здесь поверхность не обязательно должна быть плоской.

Наконец, мы можем снова интегрировать по времени т₁ к т₂, получая общее количество свойства, протекающего через поверхность за это время (т₂ − т₁):

${ displaystyle q = int _ {t_ {1}} ^ {t_ {2}} iint _ {S} mathbf {j} cdot { rm {d}} { mathbf {A}} , { rm {d}} т}$

Транспортные потоки

Восемь наиболее распространенных форм потоков из литературы по явлениям переноса определены следующим образом:

1. Импульсный поток, скорость передачи импульс на единицу площади (Н · с · м⁻²· С⁻¹). (Закон вязкости Ньютона )^[7]
2. Тепловой поток, скорость высокая температура расход через единицу площади (Дж · м⁻²· С⁻¹). (Закон проводимости Фурье )^[8] (Это определение теплового потока соответствует первоначальному определению Максвелла.)^[5]
3. Диффузионный поток, скорость движения молекул через единицу площади (моль · м⁻²· С⁻¹). (Закон диффузии Фика )^[7]
4. Объемный поток, скорость объем расход через единицу площади (м³· М⁻²· С⁻¹). (Закон Дарси о потоке грунтовых вод )
5. Поток массы, скорость масса расход через единицу площади (кг · м⁻²· С⁻¹). (Либо альтернативная форма закона Фика, которая включает молекулярную массу, либо альтернативная форма закона Дарси, которая включает плотность.)
6. Радиационный поток, количество переданной энергии в виде фотоны на определенном расстоянии от источника на единицу площади в секунду (Дж · м⁻²· С⁻¹). Используется в астрономии для определения величина и спектральный класс звезды. Также действует как обобщение теплового потока, который равен потоку излучения при ограничении электромагнитным спектром.
7. Поток энергии, скорость передачи энергия через единицу площади (Дж · м⁻²· С⁻¹). Излучательный поток и тепловой поток являются частными случаями потока энергии.
8. Поток частиц, скорость переноса частиц через единицу площади ([число частиц] m⁻²· С⁻¹)

Эти потоки являются векторами в каждой точке пространства и имеют определенную величину и направление. Также можно взять расхождение любого из этих потоков для определения скорости накопления количества в контрольном объеме вокруг заданной точки пространства. Для несжимаемый поток, расходимость объемного потока равна нулю.

Химическая диффузия

Как упоминалось выше, химический молярный поток компонента A в изотермический, изобарическая система определяется в Закон диффузии Фика так как:

${ displaystyle mathbf {J} _ {A} = - D_ {AB} nabla c_ {A}}$

где набла символ ∇ обозначает градиент оператор D_AB - коэффициент диффузии (m²· С⁻¹) компонента A, диффундирующего через компонент B, c_А это концентрация (моль / м³) компонента A.^[9]

Этот поток измеряется в моль · м.⁻²· С⁻¹, и соответствует первоначальному определению потока Максвелла.^[5]

Для разреженных газов кинетическая молекулярная теория связывает коэффициент диффузии D к плотности частиц п = N/V, молекулярная масса м, столкновение поперечное сечение ${ displaystyle sigma}$, а абсолютная температура Т от

${ displaystyle D = { frac {2} {3n sigma}} { sqrt { frac {kT} { pi m}}}}}$

где второй фактор - это длина свободного пробега и квадратный корень (с Постоянная Больцмана k) это средняя скорость частиц.

В турбулентных потоках перенос вихревым движением может быть выражен как сильно увеличенный коэффициент диффузии.

Квантовая механика

В квантовая механика, частицы массы м в квантовое состояние ψ (р, t) имеют плотность вероятности определяется как

${ Displaystyle Rho = psi ^ {*} psi = | psi | ^ {2}. ,}$

Таким образом, вероятность найти частицу в дифференциале элемент объема d³р является

${ displaystyle { rm {d}} P = | psi | ^ {2} { rm {d}} ^ {3} mathbf {r}. ,}$

Тогда количество частиц, проходящих перпендикулярно через единицу площади поперечное сечение в единицу времени - поток вероятностей;

${ displaystyle mathbf {J} = { frac {i hbar} {2m}} left ( psi nabla psi ^ {*} - psi ^ {*} nabla psi right). ,}$

Иногда это называют вероятностью тока или плотностью тока,^[10] или плотность потока вероятности.^[11]

Поток как поверхностный интеграл

Общее математическое определение (поверхностный интеграл)

Как математическое понятие поток представлен поверхностный интеграл векторного поля,^[12]

${ Displaystyle Phi _ {F} = iint _ {A} mathbf {F} cdot mathrm {d} mathbf {A}}$

${ Displaystyle Phi _ {F} = iint _ {A} mathbf {F} cdot mathbf {n} mathrm {d} A}$

где F это векторное поле, и dА это векторная площадь поверхности А, направленный как нормальная поверхность. Во-вторых, п направлено вовне единичный вектор нормали на поверхность.

Поверхность должна быть ориентируемый, т.е. можно выделить две стороны: поверхность не загибается сама на себя. Кроме того, поверхность должна быть действительно ориентирована, то есть мы используем соглашение о том, какое направление считается положительным; обратный поток считается отрицательным.

Нормаль к поверхности обычно направляется правило правой руки.

И наоборот, можно рассматривать поток как более фундаментальную величину и называть векторное поле плотностью потока.

Часто векторное поле рисуется кривыми (линиями поля), следующими «потоку»; величина векторного поля - это плотность линий, а поток через поверхность - это количество линий. Линии исходят из областей положительного расхождение (источники) и заканчиваются в областях отрицательного расхождения (опускания).

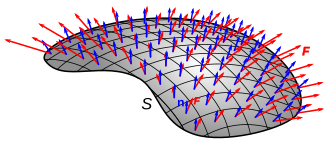
Смотрите также изображение справа: количество красных стрелок, проходящих через единицу площади, - это плотность потока, кривая обводка красных стрелок обозначает границу поверхности, а ориентация стрелок по отношению к поверхности обозначает знак внутренний продукт векторного поля с нормалями к поверхности.

Если поверхность охватывает трехмерную область, обычно поверхность ориентирована так, что приток считается положительным; наоборот выход.

В теорема расходимости утверждает, что чистый отток через замкнутую поверхность, другими словами, чистый отток из трехмерной области, находится путем добавления локального чистого оттока из каждой точки в регионе (который выражается расхождение ).

Если поверхность не замкнута, она имеет ориентированную кривую в качестве границы. Теорема Стокса заявляет, что поток завиток векторного поля - это линейный интеграл векторного поля над этой границей. Этот интеграл по путям также называется обращение, особенно в гидродинамике. Таким образом, завиток - это плотность циркуляции.

Мы можем применить поток и эти теоремы ко многим дисциплинам, в которых мы видим токи, силы и т. Д., Приложенные через области.

Электромагнетизм

Один из способов лучше понять концепцию потока в электромагнетизме - это сравнить его с сеткой для бабочек. Количество воздуха, проходящего через сеть в любой момент времени, и есть поток. Если скорость ветра высока, то поток через сеть велик. Если сеть сделать больше, то поток будет больше, даже если скорость ветра такая же. Чтобы через сетку проходила большая часть воздуха, отверстие сетки должно быть обращено в сторону ветра. Если сетка параллельна ветру, то ветер не будет двигаться через сетку. Самый простой способ представить себе поток - это «сколько воздуха проходит через сеть», где воздух - это поле скорости, а сеть - это граница воображаемой поверхности.

Электрический поток

Электрический «заряд», такой как одиночный электрон в космосе, имеет величину, определенную в кулонах. Такой заряд окружает электрическое поле. В наглядной форме электрическое поле показано в виде точки, излучающей «линии потока», называемые линиями Гаусса.^[13] Плотность электрического потока - это количество электрического потока, количество «линий», проходящих через данную область. Единицы Гаусс /квадратный метр.^[14]

Две формы электрический поток используются, один для E-поле:^[15][16]

${ displaystyle Phi _ {E} =}$ ${ displaystyle { scriptstyle A}}$ ${ Displaystyle mathbf {E} cdot { rm {d}} mathbf {A}}$

и один для D-поле (называемое электрическое перемещение ):

${ displaystyle Phi _ {D} =}$ ${ displaystyle { scriptstyle A}}$ ${ Displaystyle mathbf {D} cdot { rm {d}} mathbf {A}}$

Эта величина возникает в Закон Гаусса - в котором говорится, что поток электрическое поле E из закрытая поверхность пропорционально электрический заряд Q_А заключенный в поверхность (независимо от того, как этот заряд распределен), интегральная форма имеет следующий вид:

${ displaystyle { scriptstyle A}}$ ${ displaystyle mathbf {E} cdot { rm {d}} mathbf {A} = { frac {Q_ {A}} { varepsilon _ {0}}}}$

где ε₀ это диэлектрическая проницаемость свободного пространства.

Если учесть поток вектора электрического поля, E, для трубки рядом с точечным зарядом в поле заряда, но не содержащей его, со сторонами, образованными касательными к полю, поток для сторон равен нулю, и на обоих концах трубки имеется равный и противоположный поток. Это следствие закона Гаусса, примененного к полю обратных квадратов. Флюс для любой поверхности поперечного сечения трубки будет одинаковым. Полный поток для любой поверхности, окружающей заряд q является q/ ε₀.^[17]

В свободном пространстве электрическое перемещение дается учредительное отношение D = ε₀ E, поэтому для любой ограничивающей поверхности Dпоток поля равен заряду Q_А внутри. Здесь выражение «поток» указывает на математическую операцию, и, как можно видеть, результат не обязательно является «потоком», поскольку на самом деле ничто не течет вдоль силовых линий электрического поля.

Магнитный поток

Плотность магнитного потока (магнитное поле ) с единицей Вт / м² (Тесла ) обозначается B, и магнитный поток определяется аналогично:^[15][16]

${ displaystyle Phi _ {B} =}$ ${ displaystyle { scriptstyle A}}$ ${ Displaystyle mathbf {B} cdot { rm {d}} mathbf {A}}$

с теми же обозначениями выше. Количество возникает в Закон индукции Фарадея, где магнитный поток зависит от времени либо потому, что граница зависит от времени, либо потому, что магнитное поле зависит от времени. В интегральном виде:

${ displaystyle - { frac {{ rm {d}} Phi _ {B}} {{ rm {d}} t}} = oint _ { partial A} mathbf {E} cdot d { boldsymbol { ell}}}$

где dℓ бесконечно малый вектор линейный элемент из замкнутая кривая ${ displaystyle partial A}$, с участием величина равной длине бесконечно малый линейный элемент и направление заданный касательной к кривой ${ displaystyle partial A}$, знак которого определяется направлением интегрирования.

Скорость изменения магнитного потока через петлю из проволоки минус электродвижущая сила создан в этом проводе. Направление таково, что если позволить току проходить через провод, электродвижущая сила вызовет ток, который «противодействует» изменению магнитного поля, создавая магнитное поле, противоположное изменению. Это основа для индукторы и много электрические генераторы.

Пойнтинг флюс

Используя это определение, поток Вектор Пойнтинга S над указанной поверхностью - это скорость, с которой электромагнитная энергия течет через эту поверхность, определенная так же, как и раньше:^[16]

${ displaystyle Phi _ {S} =}$ ${ displaystyle { scriptstyle A}}$ ${ Displaystyle mathbf {S} cdot { rm {d}} mathbf {A}}$

Поток Вектор Пойнтинга через поверхность проходит электромагнитный мощность, или энергия за единицу время, проходя через эту поверхность. Это обычно используется при анализе электромагнитное излучение, но может применяться и в других электромагнитных системах.

Как ни странно, вектор Пойнтинга иногда называют поток мощности, который является примером первого использования потока выше.^[18] Он имеет единицы Вт на квадратный метр (Вт / м²).

Блоки радиометрии СИ

Блоки радиометрии СИ

Количество		Единица измерения		Размер	Заметки
имя	Символ[nb 1]	имя	Символ	Символ
Энергия излучения	Qе[nb 2]	джоуль	J	M⋅L2⋅Т−2	Энергия электромагнитного излучения.
Плотность лучистой энергии	ше	джоуль на кубический метр	Дж / м3	M⋅L−1⋅Т−2	Лучистая энергия на единицу объема.
Сияющий поток	Φе[nb 2]	ватт	W = Дж / с	M⋅L2⋅Т−3	Излучаемая, отраженная, переданная или полученная энергия излучения в единицу времени.Иногда это также называют «сияющей силой».
Спектральный поток	Φе, ν[№ 3]	ватт на герц	Вт /Гц	M⋅L2⋅Т−2	Лучистый поток на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅нм.−1.
	Φе, λ[№ 4]	ватт на метр	Вт / м	M⋅L⋅Т−3
Сияющая интенсивность	яе, Ω[№ 5]	ватт на стерадиан	Вт /SR	M⋅L2⋅Т−3	Излучаемый, отраженный, передаваемый или принимаемый поток излучения на единицу телесного угла. Это направленный количество.
Спектральная интенсивность	яе, Ω, ν[№ 3]	ватт на стерадиан на герц	W⋅sr−1⋅Гц−1	M⋅L2⋅Т−2	Интенсивность излучения на единицу частоты или длины волны. Последний обычно измеряется в W⋅sr.−1⋅нм−1. Это направленный количество.
	яе, Ω, λ[№ 4]	ватт на стерадиан на метр	W⋅sr−1⋅m−1	M⋅L⋅Т−3
Сияние	Lе, Ω[№ 5]	ватт на стерадиан на квадратный метр	W⋅sr−1⋅m−2	M⋅Т−3	Лучистый поток, излучаемый, отраженный, передаваемый или принимаемый поверхность, на единицу телесного угла на единицу площади проекции. Это направленный количество. Иногда это также ошибочно называют «интенсивностью».
Спектральное сияние	Lе, Ω, ν[№ 3]	ватт на стерадиан на квадратный метр на герц	W⋅sr−1⋅m−2⋅Гц−1	M⋅Т−2	Сияние поверхность на единицу частоты или длины волны. Последний обычно измеряется в W⋅sr.−1⋅m−2⋅нм−1. Это направленный количество. Иногда это также ошибочно называют «спектральной интенсивностью».
	Lе, Ω, λ[№ 4]	ватт на стерадиан на квадратный метр, на метр	W⋅sr−1⋅m−3	M⋅L−1⋅Т−3
Освещенность Плотность потока	Eе[nb 2]	ватт на квадратный метр	Вт / м2	M⋅Т−3	Сияющий поток получено по поверхность на единицу площади. Иногда это также ошибочно называют «интенсивностью».
Спектральная освещенность Спектральная плотность потока	Eе, ν[№ 3]	ватт на квадратный метр на герц	W⋅m−2⋅Гц−1	M⋅Т−2	Освещенность поверхность на единицу частоты или длины волны. Иногда это также ошибочно называют «спектральной интенсивностью». Внесистемные единицы спектральной плотности потока включают: Янски (1 Ян = 10−26 W⋅m−2⋅Гц−1) и блок солнечного потока (1 SFU = 10−22 W⋅m−2⋅Гц−1 = 104 Jy).
	Eе, λ[№ 4]	ватт на квадратный метр, на метр	Вт / м3	M⋅L−1⋅Т−3
Лучистость	Jе[nb 2]	ватт на квадратный метр	Вт / м2	M⋅Т−3	Сияющий поток уходящий (испускается, отражается и передается) a поверхность на единицу площади. Иногда это также ошибочно называют «интенсивностью».
Спектральное излучение	Jе, ν[№ 3]	ватт на квадратный метр на герц	W⋅m−2⋅Гц−1	M⋅Т−2	Сияние поверхность на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅м.−2⋅нм−1. Иногда это также ошибочно называют «спектральной интенсивностью».
	Jе, λ[№ 4]	ватт на квадратный метр, на метр	Вт / м3	M⋅L−1⋅Т−3
Сияющая выходность	Mе[nb 2]	ватт на квадратный метр	Вт / м2	M⋅Т−3	Сияющий поток испускается по поверхность на единицу площади. Это излучаемая составляющая излучения. «Излучение» - это старый термин для обозначения этой величины. Иногда это также ошибочно называют «интенсивностью».
Спектральная выходность	Mе, ν[№ 3]	ватт на квадратный метр на герц	W⋅m−2⋅Гц−1	M⋅Т−2	Сияющий выход поверхность на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅м.−2⋅нм−1. «Спектральный коэффициент излучения» - старый термин для обозначения этой величины. Иногда это также ошибочно называют «спектральной интенсивностью».
	Mе, λ[№ 4]	ватт на квадратный метр, на метр	Вт / м3	M⋅L−1⋅Т−3
Сияющее воздействие	ЧАСе	джоуль на квадратный метр	Дж / м2	M⋅Т−2	Лучистая энергия, полученная поверхность на единицу площади, или, что эквивалентно, освещенность поверхность интегрируется с течением времени облучения. Иногда это также называют «сияющим флюенсом».
Спектральная экспозиция	ЧАСе, ν[№ 3]	джоуль на квадратный метр на герц	J⋅m−2⋅Гц−1	M⋅Т−1	Сияющая экспозиция поверхность на единицу частоты или длины волны. Последний обычно измеряется в Дж⋅м.−2⋅нм−1. Иногда это также называют «спектральным флюенсом».
	ЧАСе, λ[№ 4]	джоуль на квадратный метр, на метр	Дж / м3	M⋅L−1⋅Т−2
Полусферический коэффициент излучения	ε	Нет данных		1	Сияющий выход поверхность, деленное на черное тело при той же температуре, что и эта поверхность.
Спектральная полусферическая излучательная способность	εν  или ελ	Нет данных		1	Спектральная выходность поверхность, деленное на черное тело при той же температуре, что и эта поверхность.
Направленная излучательная способность	εΩ	Нет данных		1	Сияние испускается по поверхность, деленное на испускаемое черное тело при той же температуре, что и эта поверхность.
Спектрально-направленная излучательная способность	εΩ, ν  или εΩ, λ	Нет данных		1	Спектральное сияние испускается по поверхность, деленное на черное тело при той же температуре, что и эта поверхность.
Полусферическое поглощение	А	Нет данных		1	Сияющий поток поглощен по поверхность, деленное на полученное этой поверхностью. Это не следует путать с "поглощение ".
Спектральное полусферическое поглощение	Аν  или Аλ	Нет данных		1	Спектральный поток поглощен по поверхность, деленное на полученное этой поверхностью. Это не следует путать с "спектральное поглощение ".
Направленное поглощение	АΩ	Нет данных		1	Сияние поглощен по поверхность, деленное на яркость, падающую на эту поверхность. Это не следует путать с "поглощение ".
Спектральное направленное поглощение	АΩ, ν  или АΩ, λ	Нет данных		1	Спектральное сияние поглощен по поверхность, деленное на спектральную яркость, падающую на эту поверхность. Это не следует путать с "спектральное поглощение ".
Полусферическое отражение	р	Нет данных		1	Сияющий поток отраженный по поверхность, деленное на полученное этой поверхностью.
Спектральная полусферическая отражательная способность	рν  или рλ	Нет данных		1	Спектральный поток отраженный по поверхность, деленное на полученное этой поверхностью.
Направленное отражение	рΩ	Нет данных		1	Сияние отраженный по поверхность, деленное на полученное этой поверхностью.
Спектральное направленное отражение	рΩ, ν  или рΩ, λ	Нет данных		1	Спектральное сияние отраженный по поверхность, деленное на полученное этой поверхностью.
Полусферический коэффициент пропускания	Т	Нет данных		1	Сияющий поток переданный по поверхность, деленное на полученное этой поверхностью.
Спектральное полусферическое пропускание	Тν  или Тλ	Нет данных		1	Спектральный поток переданный по поверхность, деленное на полученное этой поверхностью.
Направленный коэффициент пропускания	ТΩ	Нет данных		1	Сияние переданный по поверхность, деленное на полученное этой поверхностью.
Спектрально-направленное пропускание	ТΩ, ν  или ТΩ, λ	Нет данных		1	Спектральное сияние переданный по поверхность, деленное на полученное этой поверхностью.
Полусферический коэффициент затухания	μ	обратный счетчик	м−1	L−1	Сияющий поток поглощен и разбросанный по объем на единицу длины, деленную на полученный объем.
Коэффициент спектрального полусферического ослабления	μν  или μλ	обратный счетчик	м−1	L−1	Спектральный лучистый поток поглощен и разбросанный по объем на единицу длины, деленную на полученный объем.
Коэффициент направленного затухания	μΩ	обратный счетчик	м−1	L−1	Сияние поглощен и разбросанный по объем на единицу длины, деленную на полученный объем.
Коэффициент направленного спектрального ослабления	μΩ, ν  или μΩ, λ	обратный счетчик	м−1	L−1	Спектральное сияние поглощен и разбросанный по объем на единицу длины, деленную на полученный объем.
Смотрите также: SI  · Радиометрия  · Фотометрия

Смотрите также

Заметки

• Браун, Майкл, доктор философии (2010). Физика для инженерии и науки, 2-е издание. Очертания Шаума. Нью-Йорк, Торонто: McGraw-Hill Publishing. ISBN  978-0-0716-1399-6.
• Перселл, Эдвард, доктор философии (2013). Электричество и магнетизм, 3-е издание. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978110-7014022.

дальнейшее чтение

• Штауффер, П. (2006). "Flux Flummoxed: предложение для последовательного использования". Грунтовые воды. 44 (2): 125–128. Дои:10.1111 / j.1745-6584.2006.00197.x. PMID  16556188.

внешние ссылки

• Словарное определение поток в Викисловарь