Уравнение Ланжевена - Langevin equation

В физике Уравнение Ланжевена (названный в честь Поль Ланжевен ) это стохастическое дифференциальное уравнение описание временной эволюции подмножества степеней свободы. Эти степени свободы обычно представляют собой коллективные (макроскопические) переменные, изменяющиеся очень медленно по сравнению с другими (микроскопическими) переменными системы. Быстрые (микроскопические) переменные ответственны за стохастический характер уравнения Ланжевена. Одно приложение для Броуновское движение, вычисляя статистику случайного движения маленькой частицы в жидкости из-за столкновений с окружающими молекулами при тепловом движении.

Броуновское движение как прототип

Исходное уравнение Ланжевена^[1] описывает Броуновское движение, очевидно случайное движение частицы в жидкости из-за столкновений с молекулами жидкости,

{ displaystyle m { frac {d mathbf {v}} {dt}} = - lambda mathbf {v} + { boldsymbol { eta}} left (t right).}

Интересующие нас степени свободы - это скорость ${ displaystyle mathbf {v}}$ частицы, ${ displaystyle m}$ обозначает массу частицы. Сила, действующая на частицу, записывается как сумма вязкой силы, пропорциональной скорости частицы (Закон Стокса ), а шумовой термин ${ Displaystyle { boldsymbol { eta}} left (т right)}$ (название, данное в физическом контексте терминам стохастических дифференциальных уравнений, которые случайные процессы ), представляющий эффект столкновений с молекулами жидкости. Сила ${ Displaystyle { boldsymbol { eta}} left (т right)}$ имеет Гауссово распределение вероятностей с корреляционной функцией

{ displaystyle left langle eta _ {i} left (t right) eta _ {j} left (t ^ { prime} right) right rangle = 2 lambda k_ {B} T delta _ {i, j} delta left (tt ^ { prime} right),}

где ${ displaystyle k_ {B}}$ является Постоянная Больцмана, ${ displaystyle T}$ это температура и ${ Displaystyle эта _ {я} влево (т вправо)}$ - i-я компонента вектора ${ Displaystyle { boldsymbol { eta}} left (т right)}$ . В ${ displaystyle delta}$ -функция форма корреляции во времени означает, что сила в момент времени ${ displaystyle t}$ предполагается, что она полностью не коррелирует с силой в любое другое время. Это приблизительное значение; реальная случайная сила имеет ненулевое время корреляции, соответствующее времени столкновения молекул. Однако уравнение Ланжевена используется для описания движения «макроскопической» частицы в гораздо более длительном масштабе времени, и в этом пределе ${ displaystyle delta}$ -корреляция и уравнение Ланжевена становится практически точным.

Другой прототипной чертой уравнения Ланжевена является наличие коэффициента затухания ${ displaystyle lambda}$ в корреляционной функции случайной силы, факт, также известный как Соотношение Эйнштейна.

Математические аспекты

Строго ${ displaystyle delta}$ -коррелированная флуктуирующая сила ${ Displaystyle { boldsymbol { eta}} left (т right)}$ не является функцией в обычном математическом смысле и даже производной ${ displaystyle d mathbf {v} / dt}$ не определяется в этом пределе. Эта проблема исчезает, когда уравнение Ланжевена записывается в интегральной форме ${ Displaystyle м mathbf {v} = int ^ {t} left (- lambda mathbf {v} + { boldsymbol { eta}} left (t right) right) dt,}$ а уравнение Ланжевена всегда следует интерпретировать как сокращение от его интеграла по времени. Общий математический термин для уравнений этого типа: "стохастическое дифференциальное уравнение ".

Другая математическая неоднозначность возникает для (довольно специфических) уравнений Ланжевена с мультипликативным шумом, то есть таких терминов, как ${ displaystyle | { boldsymbol {v}} (t) | { boldsymbol { eta}} (t)}$ на правой стороне .. Такие уравнения могут быть интерпретированы в соответствии со схемой Стратоновича или Ито, и если вывод уравнения Ланжевена не говорит, какое из них использовать, это в любом случае сомнительно. Увидеть It исчисление.^[2]

Общее уравнение Ланжевена

Существует формальный вывод типичного уравнения Ланжевена из классической механики.^[3]^[4] Это уравнение общего положения играет центральную роль в теории критическая динамика,^[5] и другие области неравновесной статистической механики. Вышеприведенное уравнение броуновского движения является частным случаем.

Обязательным условием вывода является критерий разделения степеней свободы на категории медленных и быстрых. Например, локальное термодинамическое равновесие в жидкости достигается за несколько времен столкновения. Но требуется гораздо больше времени для релаксации плотности сохраняющихся величин, таких как масса и энергия, до равновесия. Таким образом, плотности консервативных величин и, в частности, их длинноволновые компоненты являются кандидатами для медленной переменной. Технически это разделение реализовано с помощью Оператор проекции Цванцига,^[6] важный инструмент в выводе. Вывод не является полностью строгим, потому что он опирается на (правдоподобные) предположения, аналогичные предположениям, требуемым где-либо еще в базовой статистической механике.

Позволять ${ Displaystyle А = {А_ {я} }}$ обозначают медленные переменные. Тогда общее уравнение Ланжевена выглядит так:

{ displaystyle { frac {dA_ {i}} {dt}} = k_ {B} T sum limits _ {j} { left [{A_ {i}, A_ {j}} right] { frac {{d} { mathcal {H}}} {dA_ {j}}}} - sum limits _ {j} { lambda _ {i, j} left (A right) { frac { d { mathcal {H}}} {dA_ {j}}} +} sum limits _ {j} { frac {d { lambda _ {i, j} left (A right)}} { dA_ {j}}} + eta _ {i} left (t right).}

Колеблющаяся сила ${ Displaystyle эта _ {я} влево (т вправо)}$ подчиняется Гауссово распределение вероятностей с корреляционной функцией

{ displaystyle left langle { eta _ {i} left (t right) eta _ {j} left (t ^ { prime} right)} right rangle = 2 lambda _ { i, j} left (A right) delta left (tt ^ { prime} right).}

Отсюда следует Отношение взаимности Онзагера ${ displaystyle lambda _ {я, j} = lambda _ {j, i}}$ для коэффициентов демпфирования ${ displaystyle lambda}$ . Зависимость ${ displaystyle d lambda _ {i, j} / dA_ {j}}$ из ${ displaystyle lambda}$ на ${ displaystyle A}$ в большинстве случаев незначительна. ${ Displaystyle { mathcal {H}} = - ln left (p_ {0} right)}$ обозначает гамильтониан системы, где ${ displaystyle p_ {0} left (A right)}$ - равновесное распределение вероятностей переменных ${ displaystyle A}$ . В заключение, ${ displaystyle [A_ {i}, A_ {j}]}$ это проекция Скобка Пуассона медленных переменных ${ displaystyle A_ {i}}$ и ${ displaystyle A_ {j}}$ на пространство медленных переменных.

В случае броуновского движения было бы ${ Displaystyle { mathcal {H}} = mathbf {p} ^ {2} / left (2mk_ {B} T right)}$ , ${ Displaystyle А = { mathbf {p} }}$ или ${ Displaystyle А = { mathbf {x}, mathbf {p} }}$ и ${ displaystyle [x_ {i}, p_ {j}] = delta _ {i, j}}$ . Уравнение движения ${ displaystyle d mathbf {x} / dt = mathbf {p} / m}$ для ${ displaystyle mathbf {x}}$ точно, нет колеблющейся силы ${ displaystyle eta _ {x}}$ и без коэффициента демпфирования ${ displaystyle lambda _ {x, p}}$ .

Примеры

Траектории свободных броуновских частиц

Рассмотрим свободную частицу массы ${ displaystyle m}$ с уравнением движения, описываемым

{ displaystyle m { frac {d mathbf {v}} {dt}} = - { frac { mathbf {v}} { mu}} + { boldsymbol { eta}} (t),}

где ${ Displaystyle mathbf {v} = d mathbf {r} / dt}$ - скорость частицы, ${ displaystyle mu}$ - подвижность частиц, а ${ Displaystyle { boldsymbol { eta}} (т) = м mathbf {а} (т)}$ представляет собой быстро флуктуирующую силу, среднее время которой обращается в нуль в характерном временном масштабе ${ displaystyle t_ {c}}$ столкновений частиц, т.е. ${ Displaystyle { overline {{ boldsymbol { eta}} (т)}} = 0}$ . Общее решение уравнения движения:

{ displaystyle mathbf {v} (t) = mathbf {v} (0) e ^ {- t / tau} + int _ {0} ^ {t} mathbf {a} (t ') e ^ {- (т-т ') / тау} дт',}

где ${ Displaystyle тау = м му}$ - время релаксации броуновского движения. Как и следовало ожидать из случайного характера броуновского движения, средняя скорость дрейфа ${ displaystyle langle mathbf {v} (t) rangle = mathbf {v} (0) e ^ {- t / tau}}$ быстро спадает до нуля при ${ Displaystyle т gg тау}$ . Также можно показать, что автокорреляционная функция скорости частицы ${ displaystyle mathbf {v}}$ дан кем-то^[7]

Смоделированные квадраты смещений свободных броуновских частиц (полупрозрачные волнистые линии) как функции времени для трех выбранных вариантов начального квадрата скорости, которые равны 0, 3kT / m и 6kT / m соответственно, причем 3kT / m является равнораспределенным значением в тепловом равновесии. Цветные сплошные кривые обозначают среднеквадратичные смещения для соответствующих выбранных параметров.

{ displaystyle { begin {align} R_ {vv} (t_ {1}, t_ {2}) & Equiv langle mathbf {v} (t_ {1}) cdot mathbf {v} (t_ { 2}) rangle & = v ^ {2} (0) e ^ {- (t_ {1} + t_ {2}) / tau} + int _ {0} ^ {t_ {1}} int _ {0} ^ {t_ {2}} R_ {aa} (t_ {1} ', t_ {2}') e ^ {- (t_ {1} + t_ {2} -t_ {1} ' -t_ {2} ') / tau} dt_ {1}' dt_ {2} ' & simeq v ^ {2} (0) e ^ {- | t_ {2} -t_ {1} | / tau} + { bigg [} { frac {3k_ {B} T} {m}} - v ^ {2} (0) { bigg]} { Big [} e ^ {- | t_ {2 } -t_ {1} | / tau} -e ^ {- (t_ {1} + t_ {2}) / tau} { Big]}, end {выровнено}}}

где мы использовали свойство, что переменные ${ Displaystyle mathbf {а} (т_ {1} ')}$ и ${ Displaystyle mathbf {а} (т_ {2} ')}$ стать некоррелированными для временных интервалов ${ displaystyle t_ {2} '- t_ {1}' gg t_ {c}}$ . Кроме того, ценность ${ displaystyle lim _ {t to infty} langle v ^ {2} (t) rangle = lim _ {t to infty} R_ {vv} (t, t)}$ устанавливается равным ${ displaystyle 3k_ {B} Т / м}$ так что он подчиняется теорема о равнораспределении. Обратите внимание, что если система изначально находится в тепловом равновесии уже с ${ displaystyle v ^ {2} (0) = 3k_ {B} Т / м}$ , тогда ${ Displaystyle langle v ^ {2} (т) rangle = 3k_ {B} Т / м}$ для всех ${ displaystyle t}$ , что означает, что система все время остается в равновесии.

Скорость ${ Displaystyle mathbf {v} (т)}$ броуновской частицы можно проинтегрировать, чтобы получить ее траекторию (при условии, что она изначально находится в начале координат)

{ displaystyle mathbf {r} (t) = mathbf {v} (0) tau { big (} 1-e ^ {- t / tau} { big)} + tau int _ { 0} ^ {t} mathbf {a} (t ') { Big [} 1-e ^ {- (t-t') / tau} { Big]} dt '.}

Следовательно, результирующее среднее смещение ${ displaystyle langle mathbf {r} (t) rangle = mathbf {v} (0) tau { big (} 1-e ^ {- t / tau} { big)}}$ асимптоты к ${ Displaystyle mathbf {v} (0) тау}$ когда система расслабляется и берет верх случайность. В дополнение среднеквадратичное смещение можно определить аналогично предыдущему вычислению как

{ displaystyle langle r ^ {2} (t) rangle = v ^ {2} (0) tau ^ {2} { big (} 1-e ^ {- t / tau} { big) } ^ {2} - { frac {3k_ {B} T} {m}} tau ^ {2} { big (} 1-e ^ {- t / tau} { big)} { big (} 3-e ^ {- t / tau} { big)} + { frac {6k_ {B} T} {m}} tau t.}

Видно, что ${ displaystyle langle r ^ {2} (t ll tau) rangle simeq v ^ {2} (0) t ^ {2}}$ , что указывает на то, что движение броуновских частиц на временах намного короче, чем время релаксации ${ Displaystyle тау}$ системы составляет (приблизительно) обращение времени инвариантный. С другой стороны, ${ Displaystyle langle r ^ {2} (t gg tau) rangle simeq 6k_ {B} T tau t / m = 6 mu k_ {B} Tt = 6Dt}$ , что предполагает, что длительное случайное движение броуновских частиц является необратимый диссипативный процесс. Здесь мы использовали Соотношение Эйнштейна – Смолуховского ${ Displaystyle D = { mu , k_ {B} T}}$ , где ${ displaystyle D}$ - коэффициент диффузии жидкости.

Этот график соответствует решениям полного уравнения Ланжевена, полученным с помощью Метод Эйлера – Маруямы. На левой панели показана временная эволюция фазового портрета гармонического осциллятора при различных температурах. На правой панели показаны соответствующие распределения вероятностей равновесия. При нулевой температуре скорость быстро спадает от своего начального значения (красная точка) до нуля из-за затухания. Для ненулевых температур скорость может быть увеличена до значений, превышающих начальное значение из-за тепловых флуктуаций. На больших временах скорость остается отличной от нуля, а распределение положения и скорости соответствует тепловому равновесию.

Гармонический осциллятор в жидкости

{ displaystyle m { frac {dv} {dt}} = - lambda v + eta (t) -kx}

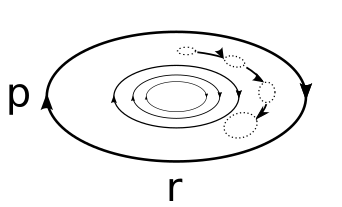
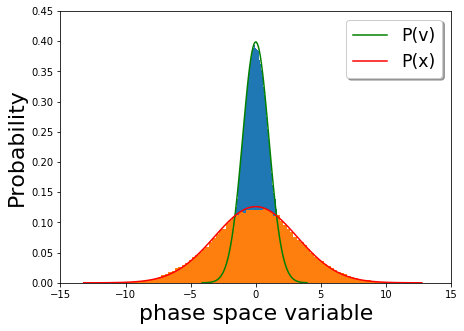
Частица в жидкости также описывается уравнением Ланжевена с потенциалом, демпфирующей силой и тепловыми флуктуациями, задаваемыми уравнением теорема о диссипации флуктуаций. Если потенциал является потенциалом гармонического осциллятора, то кривые постоянной энергии представляют собой эллипсы, как показано на рисунке 1 ниже. Однако при наличии силы диссипации частица продолжает терять энергию в окружающую среду. С другой стороны, тепловая флуктуация случайным образом добавляет энергии частице. В отсутствие тепловых флуктуаций частица непрерывно теряет кинетическую энергию и фазовый портрет временной эволюции скорости в зависимости от положения выглядит как эллипс, который закручивается по спирали, пока не достигает нулевой скорости. И наоборот, тепловые флуктуации вызывают толчки частиц, которые не позволяют частице терять всю свою энергию. Таким образом, в долгое время первоначальный ансамбль стохастических осцилляторов расширялся, в конечном итоге тепловое равновесие, для которых распределение скорости и положения задается Распределение Максвелла – Больцмана. На графике ниже (Рисунок 2) долгосрочное распределение скорости (оранжевый) и распределение положения (синий) в гармоническом потенциале ( ${ displaystyle U = { frac {1} {2}} kx ^ {2}}$ ) построен с вероятностями Больцмана для скорости (красный) и положения (зеленый). Мы видим, что поведение на позднем этапе отражает тепловое равновесие.

Рисунок 2: Вероятность равновесия для динамики Ланжевена в гармоническом потенциале

Электрическая цепь, состоящая из резистора и конденсатора.

Тепловой шум в электрическом резисторе

Существует близкая аналогия между парадигматической броуновской частицей, рассмотренной выше, и Джонсон шум, электрическое напряжение, создаваемое тепловыми колебаниями в каждом резисторе.^[8] На схеме справа показана электрическая цепь, состоящая из сопротивление р и емкость C. Медленная переменная - это напряжение U между концами резистора. Гамильтониан читается ${ Displaystyle { mathcal {H}} = E / k_ {B} T = CU ^ {2} / (2k_ {B} T)}$ , и уравнение Ланжевена принимает вид

{ displaystyle { frac {dU} {dt}} = - { frac {U} {RC}} + eta left (t right), ; ; left langle eta left (t right) eta left (t ^ { prime} right) right rangle = { frac {2k_ {B} T} {RC ^ {2}}} delta left (tt ^ { prime }верно).}

Это уравнение можно использовать для определения корреляционной функции

{ displaystyle left langle U left (t right) U left (t ^ { prime} right) right rangle = left (k_ {B} T / C right) exp left (- left vert tt ^ { prime} right vert / RC right) приблизительно 2Rk_ {B} T delta left (tt ^ { prime} right),}

который становится белым шумом (шум Джонсона), когда емкость C становится пренебрежимо малой.

Критическая динамика

Динамика параметр порядка ${ displaystyle varphi}$ фазового перехода второго рода замедляется вблизи критическая точка и может быть описан уравнением Ланжевена.^[5] Самый простой случай - это класс универсальности «модель A» с несохраняющимся скалярным параметром порядка, реализованная, например, в аксиальных ферромагнетиках,

{ displaystyle { begin {align} { frac { partial varphi left ( mathbf {x}, t right)} { partial t}} & = - lambda { frac { delta { mathcal {H}}} { delta varphi}} + eta left ( mathbf {x}, t right), { mathcal {H}} & = int d ^ {d} x left {{ frac {1} {2}} varphi left [r_ {0} - nabla ^ {2} right] varphi + u varphi ^ {4} right }, left langle eta left ( mathbf {x}, t right) eta left ( mathbf {x} ', t' right) right rangle & = 2 lambda delta left ( mathbf {x} - mathbf {x} ' right) delta left (t-t' right). end {выравнивается}}}

Другие классы универсальности (номенклатура «модель A», ..., «модель J») содержат рассеивающий параметр порядка, параметры порядка с несколькими компонентами, другие критические переменные и / или вклады скобок Пуассона.^[5]

Восстановление статистики Больцмана

Уравнения Ланжевена должны воспроизводить Распределение Больцмана. 1-мерный чрезмерно демпфированный Поучительный пример - броуновское движение. Случай сверхдемпфирования реализуется, когда инерция частицы незначительна по сравнению с демпфирующей силой. Траектория ${ Displaystyle х (т)}$ частицы в потенциале ${ Displaystyle V (х)}$ описывается уравнением Ланжевена

{ displaystyle lambda { frac {dx} {dt}} = - { frac { partial V (x)} { partial x}} + eta (t),}

где шум характеризуется ${ displaystyle left langle eta (t) eta (t ') right rangle = 2k_ {B} T lambda delta (t-t')}$ и ${ displaystyle lambda}$ - постоянная затухания. Мы хотели бы вычислить распределение ${ displaystyle p (x)}$ положения частицы с течением времени. Прямой способ определить это распределение - ввести тестовую функцию ${ displaystyle f}$ , и посмотреть на среднее значение этой функции по всем реализациям (среднее по ансамблю)

{ displaystyle lambda { frac {d left langle f (x (t)) right rangle} {dt}} = left langle f '(x (t)) lambda { frac {dx } {dt}} right rangle = left langle -f '(x (t)) { frac { partial V} { partial x}} + f' (x (t)) eta (t ) right rangle.}

Если ${ Displaystyle х (т)}$ остается конечным, то эта величина равна нулю. Более того, используя интерпретацию Стратоновича, мы можем избавиться от эта во втором члене, так что в итоге мы получим

{ displaystyle left langle -f '(x) { frac { partial V} { partial x}} + k_ {B} Tf' '(x) right rangle = 0,}

где мы используем функцию плотности вероятности ${ displaystyle p (x)}$ . Это делается путем явного вычисления среднего,

{ displaystyle int left (-f '(x) { frac { partial V} { partial x}} p (x) + {k_ {B} T} f' '(x) p (x) right) dx = int left (-f '(x) { frac { partial V} { partial x}} p (x) - {k_ {B} T} f' (x) p '( x) right) dx = 0,}

где второй член интегрирован по частям (отсюда отрицательный знак). Поскольку это верно для произвольных функций ${ displaystyle f}$ , мы должны иметь:

{ displaystyle { frac { partial V} { partial x}} p (x) + {k_ {B} T} p '(x) = 0,}

таким образом восстанавливая распределение Больцмана

{ displaystyle p (x) propto exp left ({- { frac {V (x)} {k_ {B} T}}} right).}

Эквивалентные методы

Решение уравнения Ланжевена для конкретной реализации флуктуирующей силы само по себе не представляет интереса; интерес представляют корреляционные функции медленных переменных после усреднения по флуктуирующей силе. Такие корреляционные функции также могут быть определены другими (эквивалентными) методами.

Уравнение Фоккера – Планка

А Уравнение Фоккера – Планка является детерминированным уравнением для зависящей от времени плотности вероятности ${ Displaystyle Р влево (А, т вправо)}$ стохастических переменных ${ displaystyle A}$ . Уравнение Фоккера – Планка, соответствующее общему уравнению Ланжевена, приведенному выше, может быть получено стандартными методами (см., Например, исх.^[9]),

{ displaystyle { frac { partial P left (A, t right)} { partial t}} = sum _ {i, j} { frac { partial} { partial A_ {i}} } left (-k_ {B} T left [A_ {i}, A_ {j} right] { frac { partial { mathcal {H}}} { partial A_ {j}}} + лямбда _ {i, j} { frac { partial { mathcal {H}}} { partial A_ {j}}} + lambda _ {i, j} { frac { partial} { partial A_ {j}}} right) P left (A, t right).}

Равновесное распределение ${ Displaystyle P (A) = p_ {0} (A) = { text {const}} times exp (- { mathcal {H}})}$ является стационарным решением.

Интеграл по пути

А интеграл по путям эквивалентное уравнению Ланжевена может быть получено из соответствующих Уравнение Фоккера – Планка или преобразовав гауссово распределение вероятностей ${ Displaystyle P ^ {( eta)} ( eta) d eta}$ колеблющейся силы ${ displaystyle eta}$ к распределению вероятностей медленных переменных, схематично ${ Displaystyle P (A) dA = P ^ {( eta)} ( eta (A)) det (d eta / dA) dA}$ Функциональный детерминант и связанные с ним математические тонкости выпадают, если уравнение Ланжевена дискретизируется естественным (причинным) способом, где ${ Displaystyle А (т + дельта т) -А (т)}$ зависит от ${ Displaystyle А (т)}$ но не на ${ Displaystyle А (т + Дельта т)}$ . Оказывается, удобно ввести вспомогательные переменные ответа ${ displaystyle { tilde {A}}}$ . Тогда интеграл по путям, эквивалентный общему уравнению Ланжевена, имеет вид^[10]

{ Displaystyle int P (A, { тильда {A}}) , dA , d { tilde {A}} = N int exp left (L (A, { tilde {A}}) ) right) dA , d { tilde {A}},}

где ${ displaystyle N}$ коэффициент нормализации и

{ displaystyle L (A, { tilde {A}}) = int sum _ {i, j} left {{ tilde {A}} _ {i} lambda _ {i, j} { tilde {A}} _ {j} - { widetilde {A}} _ {i} left { delta _ {i, j} { frac {dA_ {j}} {dt}} - k_ { B} T left [A_ {i}, A_ {j} right] { frac {d { mathcal {H}}} {dA_ {j}}} + lambda _ {i, j} { frac {d { mathcal {H}}} {dA_ {j}}} - { frac {d lambda _ {i, j}} {dA_ {j}}} right } right } dt.}

Формулировка интеграла по путям не добавляет ничего нового, но позволяет использовать инструменты из квантовая теория поля; например методы возмущения и ренормгруппы (если они имеют смысл).

Смотрите также

Динамика Ланжевена

использованная литература

^ Ланжевен, П. (1908). "Sur la théorie du mouvement brownien [К теории броуновского движения]". C. R. Acad. Sci. Париж. 146: 530–533.; обзор D. S. Lemons & A. Gythiel: Статья Поля Ланжевена 1908 года «О теории броуновского движения» [...], Являюсь. J. Phys. 65, 1079 (1997), Дои:10.1119/1.18725
^ Случайные процессы в физике и химии. Эльзевир. 2007 г. Дои:10.1016 / b978-0-444-52965-7.x5000-4. ISBN 978-0-444-52965-7.
^ Кавасаки, К. (1973). «Простые выводы обобщенных линейных и нелинейных уравнений Ланжевена». J. Phys. A: Математика. Nucl. Gen. 6 (9): 1289–1295. Bibcode:1973JPhA .... 6,1289K. Дои:10.1088/0305-4470/6/9/004.
^ Денглер, Р. (2015). «Другой вывод обобщенных уравнений Ланжевена». arXiv:1506.02650v2 [Physics.class-ph ].
^ ^а ^б ^c Hohenberg, P.C .; Гальперин, Б.И. (1977). «Теория динамических критических явлений». Обзоры современной физики. 49 (3): 435–479. Bibcode:1977РвМП ... 49..435Н. Дои:10.1103 / RevModPhys.49.435.
^ Zwanzig, R. (1961). «Эффекты памяти в необратимой термодинамике». Phys. Ред. 124 (4): 983–992. Bibcode:1961ПхРв..124..983З. Дои:10.1103 / PhysRev.124.983.
^ Патрия РК (1972). Статистическая механика. Оксфорд: Pergamon Press. С. 443, 474–477. ISBN 0-08-018994-6.
^ Джонсон, Дж. (1928). «Тепловое возбуждение электричества в проводниках». Phys. Rev. 32 (1): 97. Bibcode:1928PhRv ... 32 ... 97J. Дои:10.1103 / PhysRev.32.97.
^ Ичимару, С. (1973), Основные принципы физики плазмы (1-е изд.), США: Бенджамин, стр. 231, ISBN 0805387536
^ Янссен, Х. К. (1976). "Лагранжеан для классической динамики поля и ренормализационные групповые расчеты динамических критических свойств". Z. Phys. B. 23 (4): 377–380. Bibcode:1976ZPhyB..23..377J. Дои:10.1007 / BF01316547. S2CID 121216943.

дальнейшее чтение

У. Т. Коффи (Тринити-колледж, Дублин, Ирландия) и Ю. П. Калмыкова (Université de Perpignan, Франция, Уравнение Ланжевена: в приложениях к стохастическим задачам физики, химии и электротехники (Третье издание), Мировая научная серия по современной химической физике - Том 27.
Рейф, Ф. Основы статистической и теплофизики, McGraw Hill New York, 1965. См. Раздел 15.5 Уравнение Ланжевена.
Р. Фридрих, Дж. Пейнке и Ч. Реннер. Как количественно определить детерминированные и случайные влияния на статистику валютного рынка, Phys. Rev. Lett. 84, 5224 - 5227 (2000)
L.C.G. Роджерс и Д. Уильямс. Диффузии, марковские процессы и мартингалы., Кембриджская математическая библиотека, Cambridge University Press, Кембридж, переиздание 2-го (1994 г.) издания, 2000 г.

[1] Ланжевен, П. (1908). "Sur la théorie du mouvement brownien [К теории броуновского движения]". C. R. Acad. Sci. Париж. 146: 530–533.; обзор D. S. Lemons & A. Gythiel: Статья Поля Ланжевена 1908 года «О теории броуновского движения» [...], Являюсь. J. Phys. 65, 1079 (1997), Дои:10.1119/1.18725

[Stochastic_Processes_in_Physics_and_Chemistry_2007_p.-2] Случайные процессы в физике и химии. Эльзевир. 2007 г. Дои:10.1016 / b978-0-444-52965-7.x5000-4. ISBN 978-0-444-52965-7.

[Kawasaki1973-3] Кавасаки, К. (1973). «Простые выводы обобщенных линейных и нелинейных уравнений Ланжевена». J. Phys. A: Математика. Nucl. Gen. 6 (9): 1289–1295. Bibcode:1973JPhA .... 6,1289K. Дои:10.1088/0305-4470/6/9/004.

[den2015-4] Денглер, Р. (2015). «Другой вывод обобщенных уравнений Ланжевена». arXiv:1506.02650v2 [Physics.class-ph ].

[HH1977-5] а ^б ^c Hohenberg, P.C .; Гальперин, Б.И. (1977). «Теория динамических критических явлений». Обзоры современной физики. 49 (3): 435–479. Bibcode:1977РвМП ... 49..435Н. Дои:10.1103 / RevModPhys.49.435.

[6] Zwanzig, R. (1961). «Эффекты памяти в необратимой термодинамике». Phys. Ред. 124 (4): 983–992. Bibcode:1961ПхРв..124..983З. Дои:10.1103 / PhysRev.124.983.

[7] Патрия РК (1972). Статистическая механика. Оксфорд: Pergamon Press. С. 443, 474–477. ISBN 0-08-018994-6.

[8] Джонсон, Дж. (1928). «Тепловое возбуждение электричества в проводниках». Phys. Rev. 32 (1): 97. Bibcode:1928PhRv ... 32 ... 97J. Дои:10.1103 / PhysRev.32.97.

[Ichimaru1973-9] Ичимару, С. (1973), Основные принципы физики плазмы (1-е изд.), США: Бенджамин, стр. 231, ISBN 0805387536

[Janssen1976-10] Янссен, Х. К. (1976). "Лагранжеан для классической динамики поля и ренормализационные групповые расчеты динамических критических свойств". Z. Phys. B. 23 (4): 377–380. Bibcode:1976ZPhyB..23..377J. Дои:10.1007 / BF01316547. S2CID 121216943.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]